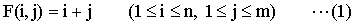
親愛なる読者諸君。
この論文に目を止めた方だ、きっと貴方は本が好きであろう。
そして、私と同じように本の整理に頭を悩ましているに違いない。
本好きなら誰でも知っていることだが、本というものは、止めどもなく増殖を続ける性質を持っている。すぐ読む本、後で読む本、後で読むつもりで結局読まない本、最初から読む気はないが安心感のために買う本、何となく集めてしまう本、惰性で買い続ける本、本、本。
本は、貴方の部屋に流砂の如くなだれこむ。しかしながら、本好きの貴方は、本を捨てることが出来ない。
押し入れの下に突っ込んでおいた段ボール箱からあふれ出し、部屋の床を蹂躙し、さらには階段から廊下まで制圧するにとどまらず、とうとう台所に植民地を築き始める、本。
こうなってしまうと、ある特定の本を探し出す作業は困難を極める。貴方は、ある本が必要になったために半日かけて蔵書の山を崩してゆかなければならない。そうして本の山を切り崩し、あらかた本の海に変えたあげく、結局のところ貴方は、その本の発掘をあきらめて、新たに1冊買ってしまうことになる。
ところが、本の海を再び山に戻してゆく最中に、ようやく探していたその本が見つかるのだ。しかも、2冊。
これではいけない。何とかしなければならない。貴方もそう思っていることだろう。私は、そのような悩みを持つ全ての方に、次のように助言したい。
本棚を買いなさい。
さて、本棚をご存じない方のために、少し本棚について説明してみよう。
本棚とは、その名の通り本を並べる棚のことである。1つの棚には、ある冊数、例えばn冊の本を並べることができる。こういう棚が複数段、例えばm段あると思って頂きたい。これが本棚の基本的な概念だ。
結果として、1つの本棚には、最大n×m冊の本が収容できることになる。この値が、本棚の収容数Pである。
ここまでの説明で、本棚の利点は明らかであろう。本棚に収容することで、本の検索が極めて容易になるのだ。
例えば、蔵書録によると、ある本が本棚の「上からj段目の棚の、左からi冊目」に置いてあると分かったとしよう。本を発見するアルゴリズムは次の通りだ。
まず棚を上から数えてゆく。j回数えたところで停止し、今度はその棚の本を左から数えてゆく。i回数えたところで停止すれば、そこにあるのが目的の本である。以上。
お分かりの通り、本の収容場所、というか座標(i,j)を記録しておけば、(i+j)回のステップで必ず発見できるわけだ。これを本の検索ステップ数と呼ぶことにする。
まあ、待ちたまえ。そんなに急いで家具店に走る必要はない。本棚を買う前にまずは本論文を最後まで読んで頂きたい。
昔からよく「本棚を見れば、持ち主の人柄が分かる」と言われてきた。本棚の選択に当たっては、くれぐれも慎重でありたいものだ。
ここでは、本棚の材質とか色とかデザインとか価格はさておき、まずは「本棚は、何よりもまず本を探す手間を最小にするような構造をしているべきである」という理念を立てて、それに従って最適な本棚の構造を考えてみることにする。
本を探す手間を最小にするというのは、すなわち前述した「本の検索ステップ数」の期待値を最小にするということだ。では、問題をきちんと表現してみよう。
1段あたりn冊の本を収容できる棚がm段から構成されている本棚があり、そこに最大収容数Pまでランダムに本を収容したとする。
ある特定の本の座標(i,j)が与えられたとき、その本の検索ステップ数の期待値を最小にするには、nとmはどのような関係にあるべきか。ただし、本の検索ステップ数 F(i,j)は次の通りであるとする。
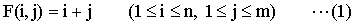
さあ、ここまでの話がよく分からなかった方も、ようやく数式が出てほっとしていることだろう。文字づらを追うのが面倒なら、以降は数式だけを見て頂いても結構である。
さて、F(i,j)の期待値はnとmの値によって決まるが、n×mは本棚の収容数Pに等しいので、次の関係が成り立つ。
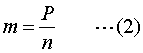
すなわち、F(i,j)の期待値は、変数nだけで決まる。これを F0(n)と表すことにしよう。すると、F0(n) は「座標(i,j)の検索ステップ数×その座標が指定される確率」を、全てのi,jの組み合わせについて合計したものに他ならない。
ところが、本はランダムに収容されると仮定したので、任意の座標が指定される確率は全て等しく1/Pである。したがって、
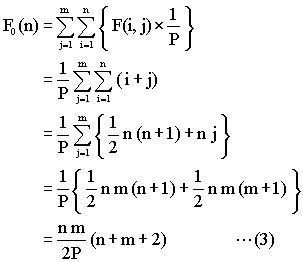
さあ、これに(2) を代入してみよう。
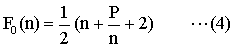
次にこの値を最小にするnの値を求める。ある関数が最小値をとるとき、その一次導関数(微分)の値は0になる。ゆえに、(4)を微分して、その値が0になる条件を見てみよう。
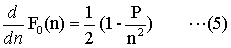
(5)より、F0(n) の微分が0となる、すなわちF0(n) が最小になる条件は、次の通りであることが分かった。
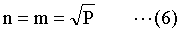
最適な本棚とは、1段あたりの本の冊数nと、段数mが等しい構造をしているものである。
ところで、読者は次のような疑問を持ったかも知れない。
「確かに、本を全て本棚に収容するという前提の下では、n=mのケースが最適解だろう。しかし、そもそも本棚に収容する方が、ただ買ってきた本を積んでおくだけより検索の手間が少ない、ということを証明してないではないか」
その通り。もしも、いわゆる「つんどく」の方が、結論Aに示された最適本棚よりも本の検索について優れているというのなら、何も本棚を買う必要はない。
そこで、両者を比較してみよう。
つんどく方式では、本の座標は1次元、すなわち上からi番目に積んである本の座標は(i)だけで表され、その検索ステップ数もiに等しい。本の冊数をnとして、つんどく方式における本の検索ステップ数の期待値F1(n)は、次のようになる。
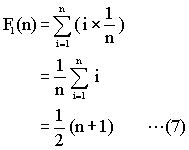
つんどく方式では、積んである本の冊数nが、すなわち最大収容数Pに等しいから、上の結果をPを変数として表すと、
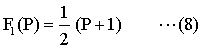
一方、最適本棚における検索ステップ数の期待値は、(4)に(6)を代入して、
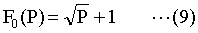
つんどく方式における本の検索ステップ数の期待値(8)が、本棚における本の検索ステップ数の期待値(9)より常に大きいことを示すには、
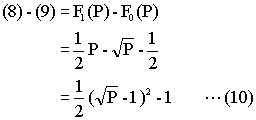
が常に0より大きいことを示せばよい。
ところが、何としたことか、(10)が正数なのはPが6以上の場合だけではないか。つまり本の冊数Pが5以下なら、つんどく方式の方が優れているのだ。
もし貴方の蔵書が6冊以上あるなら、最適本棚を購入すべきである。
そうでないのなら、ただ積んでおいた方がよい。
賢明な読者には、すでに次のことがお分かりだろう。結論Bは、本棚における棚の1つ1つについても成立するのだ。そこで、次の結論が導かれる。
本棚の1つの棚に、6冊以上の本を並べるべきではない。
6冊目以降の本は、別の棚に移動させるべきである。
すると、最適本棚のうち最も収容数が大きいものは、5冊×5段で25冊のものだということになる。さあ、これで最適本棚が明確になった。
最適本棚とは、5冊×5段で最大収容数25冊の本棚である。
しかし、貴方はまだ納得しないかも知れない。
「26冊目の本を購入したらどうすればよいのか。最適本棚を何個も並べるのか」
その通りである。ただし、お気づきのことと思うが、最適本棚を6個以上並べるべきではない。
部屋の中に、6つ以上の最適本棚を並べるべきではない。
6個目以降の最適本棚は、別の部屋に移動させるべきである。
これで、貴方の部屋、「最適書庫」の大きさが明確になった。最適書庫とは、最適本棚を5つ設置し、最大125冊の蔵書を納めることが出来る部屋である。
えっ、126冊目の本を買ってしまった?
ご安心を。複数の最適書庫を含む屋敷を建てればよいのだ。ただし・・・そう、そのような最適屋敷には、最適書庫を6部屋以上作るべきではない。
このようにして得られた最終的な結論をまとめてみよう。
正しい本の整理法は、次の通りである。
蔵書数が
1~ 5 冊の場合 : ただ積んでおく
6~25 冊の場合 : 最適本棚(5冊×5段)を購入
26~125冊の場合 : 最適書斎(最適本棚×5)を設ける
126~625冊の場合 : 最適屋敷(最適書斎×5)を建てる
626~3,125冊の場合 : 大地主となって最適屋敷×5を築く
3,126~15,625 冊の場合 : 革命を起こして国土を占拠、5分割して統治
15,626~78,125 冊の場合 : 世界5大陸を征服、支配し、本で埋めつくす
さあ、これで、誰でも自分の蔵書数に合わせて正しく本を整理できるだろう。
貴方の蔵書が、例えば1千冊あるとしよう。ほら、さきほど家具店に行くのを止めた理由が分かるだろう。正しく本を整理しようと思うのなら、貴方は家具店ではなく、不動産屋さんに行くべきなのだ。
季刊「せる」1987年秋号(通巻6号)掲載作品に加筆修正(2002年10月)
馬場秀和
馬場秀和アーカイブへ戻る